Jde o pojem vyslovovaný s úctou od antických dob podnes. Podíváme se do učebnice matematiky, do historie malířství i na fotografickou praxi. Nejdříve tedy trochu té matematiky. Matematicky vzato, je to poměr o hodnotě 1,618033988749 atd. K číslu se dojde vzorečkem 1 plus odmocnina z pěti, to celé lomeno dvěma. Uf.
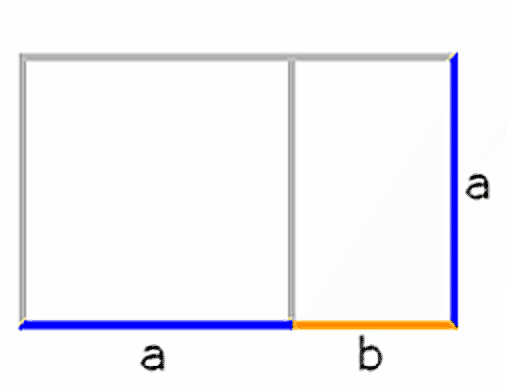
Pochopitelnější je dělení úsečky. O zlatém řezu hovoříme, když je poměr větší části k menší části stejný, jako poměr celé úsečky k větší části. Odtud pak je cesta ke zlatému obdélníku, ten je vyobrazen zde:
Jde o pojem vyslovovaný s úctou od antických dob podnes. Podíváme se do učebnice matematiky, do historie malířství i na fotografickou praxi. Nejdříve tedy trochu té matematiky. Matematicky vzato, je to poměr o hodnotě 1,618033988749 atd. K číslu se dojde vzorečkem 1 plus odmocnina z pěti, to celé lomeno dvěma. Uf.
Pochopitelnější je dělení úsečky. O zlatém řezu hovoříme, když je poměr větší části k menší části stejný, jako poměr celé úsečky k větší části. Odtud pak je cesta ke zlatému obdélníku, ten je vyobrazen zde:
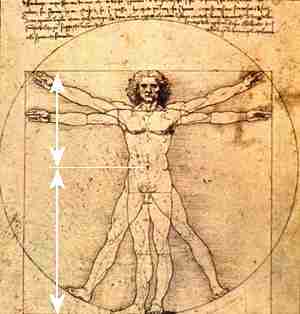
Zlatý řez objevili v Antice Řekové a řídili se jím při stavění i v sochařském umění. Na počest sochaře Feidia se onen poměr označuje písmenem fí řecké abecedy. Velmi známé jsou Leonardovy studie na toto téma:
Je to ilustrace skutečnosti, že pentagram, tedy pěticípá hvězda nakreslená jedním tahem, má vzdálenosti mezi vrcholy v poměru zlatého řezu. Zajímavá je aplikace zásad zlatého řezu na Leonardovu Monu Lisu:

A co ve fotografii?
V učebnicích se můžeme dočíst leccos o aplikaci zlatého řezu na fotografii. Čítám to od raného mládí a za tu dobu jsem si nedokázal představit, že by někdo pobíhal po place a odměřoval vzdálenosti v poměru 1:1,618. Jsou známé i analýzy klasických obrazů s ohledem na aplikaci zlatého řezu, ukázky jsou například ve Wikipedii. Nicméně připadají mi někdy hodně umělé a přitažené za vlasy. Zlatý řez v architektuře si dovedu představit, nicméně ve fotografii mi to téma připadá hodně akademické.
Nicméně, zásadní a podstatný význam přece má:
Naprosto není jedno, jak jsou objekty v ploše obrazu rozmístěny. Jako východisko jsem zvolil fotku naší Nory. Je umístěna v geometrickém středu fotky. To je místo, které je TABU. Pokud není ke středové kompozici očividní důvod, je to jasná chyba a budiž to pronásledováno a pranýřováno.

Aplikujme tedy na fotku pravidlo zlatého řezu. Zde vidíte klasický diagram, vidíte, že se obdélníčky zmenšují a dovedete si představit, že se to zmenšování děje po jakési spirále, tak to opravdu je, v této souvislosti se hovoří o Fibonacciho posloupnosti, je to vidět i v přírodě, například podobně se zmenšují závity šnečí ulity.

Toto je týž obrázek, kde hlava Nory je umístěna důsledně podle pravidla zlatého řezu.

Upřímně se mi to nelíbí. Nedovedu to argumentovat, ale připadá mi, že je pes vražený do kouta a před sebou že má zbytečně velký prostor. Sám se tedy v praxi na zlatý řez neohlížím: vypočítat ho neumím, a jeho aplikace na fotku mi připadá umělá. Držím se praktičtějšího pravidla třetin: plocha fotky je dělena na třetiny, tedy jsou zde v třetinách dvě osy svislé a dvě vodorovné. Tam, kde se protínají, je silný obrazový bod, celkově tedy jsou čtyři. Jakmile umístíme motiv do silného obrazového bodu, je nakročeno k dobré kompozici.

Takhle to pak vypadá bez té mřížky:

Nicméně i pak mi tu něco skřípe. Pes má kolem sebe zbytečně velký prostor. Přiblížím se tedy motivu, a k pravidlu třetin přidám další pravidlo, které jsem si stanovil:
Málo nad hlavou, oči nad vodorovnou osou, pod nohama větší místo než nad hlavou.

Pak ovšem hlava psa je NAD silným obrazovým bodem. Důležité ale je, že osa hlavy a hrudi pořád běží po té svislé třetině. Pravidlo „málo nad hlavou“ je pro mě nadřazené poučce o silném obrazovém bodu.

No a takto si myslím, že je to v pořádku,motiv, tedy to, co fotím, by měl vyplňovat významnou část plochy a to se zde děje. Od matematiky jsme se tedy dostali k praxi. Je to samozřejmě diskutabilní a dovedu si představit, že se někdo opravdu zlatého řezu drží a dosahuje skvělých výsledků. Přesto si myslím, že pro praxi je vodítko v podobě mřížky složené z třetin praktičtější a že vede k dobrým výsledkům.